The rhombus is a quadrilateral whose all sides are equal, and diagonals intersect each other at 90 degrees. Rhombus is a diamond shape quadrilateral. Some also call the rhombus a special kind of parallelogram.
In mathematics, there are a lot of questions regarding a rhombus.
Rhombus formula
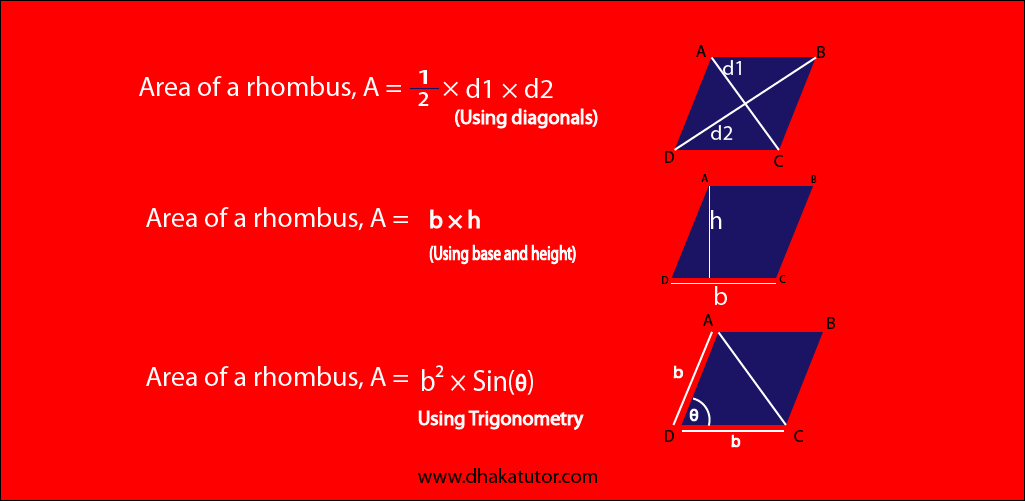
|
When both diagonals are given |
A = ½ × d1 × d2 |
|
When base and height are given |
A = b × h |
|
When angle is given |
A = b2 × Sin(a) |
Finding area of a Rhombus:
If “b” is its sides and “θ” is an included angle, the formula is: Area of a Rhombus = b2 sin θ square units.
Example: The length of a side of a rhombus is 9cm, and the included angle is 30 degrees. Then the area should be 92 sin 30 square units. The area is 40.5 square units.
There are other ways to find the area of a rhombus too.
One of the ways is by using the formula D1 x D2/2. D1 and D2 are the values of the diagonal.
Example: The length of Diagonal 1 is 6cm, and the length of Diagonal 2 is 8cm. Putting it into the formula should give us 6 x 8/2, which are 24 units squared.